
LTV. Интегралы и площади?
Часто случается так, что имея в наличии необходимый инструмент для расчета какого-либо показателя, человек использует его «на веру». Если известна его функция, то зачем углубляться в происхождение? Такой подход я считаю в корне неправильным. Специалист должен стремиться к улучшению своих профессиональных навыков, разбираться в базовых и основополагающих моментах, ведь с этими знаниями придет возможность модифицировать и улучшать используемые методы.
Итак, напомню, что такое LTV (англ. Lifetime Value). Фактически это доход с одного пользователя за время его существования в проекте. Знание LTV позволит оценить окупаемость инвестиций (ROI), определить лучшие каналы трафика и т.п.
Безусловно, время «жизни» в игре у каждого пользователя разное, как и количество внесенных средств, поэтому целесообразно взять среднее время жизни игрока (LT) и средний доход в день (ARPDAU) .
Из всего вышесказанного вытекает метод прогнозирования LTV, основывающийся на знании среднего времени жизни LT и дохода с одного пользователя в день.
Интегральные функции распределения (Функции отвала и удержания)
Рассмотрим некоторую неотрицательную непрерывную случайную величину t, которая является временем до возникновения интересующего нас события, а именно до «смерти» — отвала пользователя. Плотность вероятности этой величины обозначим f(t).Как будет показано позднее, вид этой функции нас не интересует.
Возьмем интегральный закон распределения величины F(t). Данная функция говорит нам о вероятности того, что событие произойдет на интервале времени [0, T):
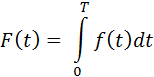
Таким образом, F(t) — функция отвала пользователя. Очевидно, значения этой функции лежат от 0 до 1. Дабы не было сомнений, рассмотрим пример. Будем отсчитывать время жизни проекта с нуля (т.е. нулевой день по факту первый день жизни проекта). Пусть в нулевой день в игру пришло N человек — вероятность отвала пользователя равна 0 (в нулевой день отвалов не происходит). В следующий день вероятность пользователя уйти составляет, например, 0.5. Умножая эту вероятность на N, мы получим количество ушедших человек.
Не трудно догадаться, что функция удержания это функция, описывающая вероятность обратного отвалу события:
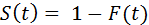
S(t) — функция удержания, которая получается путем аппроксимации наблюдательных данных Retention — Days степенной функцией (ax^b) . В общем случае, данная функция называется Survival function (функция выживаемости). Она применятся для прогнозирования исходов в медицине, социологии и т.д.
S(t) — вероятность того, что событие произойдет на интервале времени [T, +∞), т.е не произойдет на [0, T):
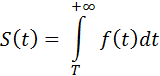
Расчет LT
Перейдем непосредственно к расчету среднего времени, на котором произойдет отвал пользователя — математическое ожидание величины t:
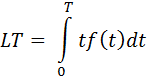
Заметим, что

Таким образом,
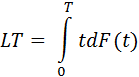
Интегрируем по частям:
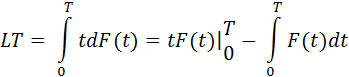
Вспомним, что вероятность отвала в нулевой день равна F(0) = 0 , а в последний день интервала F(T) = 1 (все пользователи уйдут из проекта):

Следовательно,
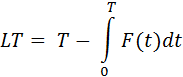
В принципе, этого уже достаточно, чтобы посчитать среднее время жизни пользователя. Но мы привыкли работать не с отвалом, а с удержанием (retention):

То есть, среднее время жизни пользователя в проекте равняется площади под функцией удержания:

Заключение. LTV
Остался последний шаг:
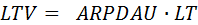
Теперь мы знаем, откуда берутся эти функции.
Одна из основных мыслей, которую я хотел донести в этой статье — используя инструмент, понимайте не только то, какой результат он выдаст, но и как он работает.
Originally published at blueshift.ru on April 9, 2016.



