Честный рандом — нечестный 

И снова здравствуй, дорогой друг. Сегодня мы расскажем занимательную историю о честности. Хорошо ли быть с игроком честными до конца или обман сулит выгоду нет? Да, ты угадал, речь пойдёт о «рандоме».

Как часто игроки рассказывают о том, что они хотят максимально честного «рандома» в твоей игре? Часто? Очень часто? Так вот, друг мой, знай — люди врут (а игроки врут всегда). Напомним одну прописную истину игрового дизайна: игроки хотят получать от игры удовольствие. Честность (если игроки это удовольствие получают в полной мере) заботит их в самую последнюю очередь.

Так что сегодня мы предлагаем перестать верить игрокам и не делать честного «рандома». Как минимум, в тех случаях, когда необходимо совершить бинарный выбор (т.е. определить: успех или неудача постигли игрока). Например, при выборе: выпал ли игроку предмет с убитого им монстра, или нет. О более сложных случаях (когда выбор производится из N вариантов) поговорим в другой статье, хотя если ты смелый, ловкий и умелый метод из этой статьи при должной сообразительности можно применить и к ним.

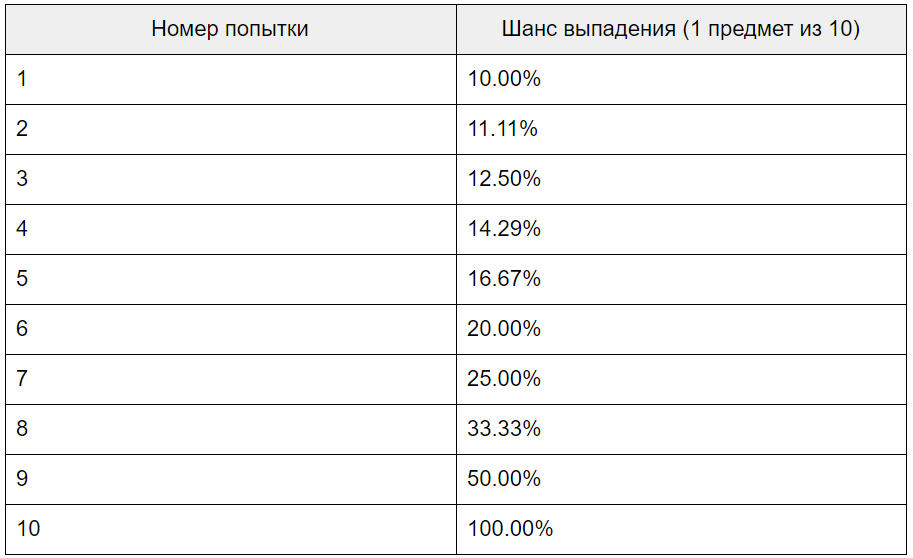
Представим себе неискушенного в игровых механиках программиста, который реализует по твоей просьбе проверку вероятности. Как он скорее всего поступит? Возьмёт стандартную функцию (какой-нибудь rand(), random() или math.random() в зависимости от того, на каком языке программирования он пишет), получит случайное число от 0 до 1, умножит его на 100 и сравнит полученный результат с указанным тобой шансом выпадения (например, с 10%). После чего со спокойной душой пойдёт дальше смотреть ютуб заниматься важными архитектурными задачами. Устроит ли тебя такой вариант? Если ты будешь смотреть только на сводную статистику выпадения этого предмета — скорее всего решишь, что устроит. Ведь ты увидишь, что в целом примерно на каждые 10 попыток игроки (вот здесь будь внимателен, не игрок, а игроки) получают 1 предмет (хотя скорее всего, конечно, ты увидишь, как на каждый 1.000.000 попыток игроки получают 100.000 предметов). Что, казалось бы, хорошо, ведь этого ты и добивался. Однако не спеши успокаиваться и бросать читать эту статью. Потому что сейчас мы покажем тебе отличную картинку, иллюстрирующую, какие чувства ты испытаешь, когда отвлечёшься от общей статистики и опустишься до рассмотрения судеб отдельных игроков (а это в целом надо делать как можно чаще, вот тебе вторая прописная истина). Вот эта картинка.

Спустившись до рассмотрения каждого конкретного игрока, ты увидишь, как много среди них тех, кто не получает предмет за 15 и даже 20 попыток, или получает предмет каждые 5-6 раз. Да, но, можешь сказать ты, пройдёт время, и кривая «рандома» всех уравняет. Бесспорно, ответим мы тебе, однако здесь и сейчас одна часть твоих игроков слишком несчастна, а вторая чересчур счастлива. Проще говоря, часть твоей аудитории испытывает ненужный тебе дефицит предметов, а часть — ненужный тебе профицит (но в среднем все едят голубцы счастливы). А это явно грозит тем, что первая часть перейдёт в категорию ушедших игроков, а вторая заплатит меньше, чем ты рассчитываешь (и ещё неясно, что из этого хуже).

Вся эта вопиющая несправедливость складывается по одной простой причине — события «N попыток выдачи игроку предмета» для одного конкретного игрока не являются зависимыми. Это означает, что каждый раз шанс получить предмет для игрока неизменен, и, допустим, 100-я подряд неуспешная попытка ни на йоту не повышает шанса успеха 101-й. При том, что подавляющее большинство твоей аудитории считает обратное — если не повезло сейчас, значит с большей вероятностью повезёт потом; однако никакой гарантии, что это «потом» наступит, ты на самом деле дать не можешь. Как же исправить эту ужасную ситуацию, спросишь ты? Отличный вопрос, садись и записывай: необходимо использовать вместо честного «рандома» нечестный, который заставит шанс выпадения предмета вести себя именно так, как представляют себе игроки, не изменяя при этом глобальной статистики «1 предмет на 10 попыток». Никакие твои расчеты от этого не пострадают, а ожидания игроков наконец-то совпадут с реальностью (что всегда хорошо, вот тебе третья прописная истина).

Итак, мы добрались до самого важного места в статье (это не значит, что тебе не надо было читать весь предыдущий текст!). Но если ты всё-таки не читал (или читал по диагонали), напомним — мы пришли к выводу, что нам необходимо корректировать шанс выпадения предмета персонально для каждого конкретного игрока в зависимости от того, сколько неуспешных попыток выпадения этого предмета было у него до того. Для этого мы придумали вот такую формулу, по которой тебе необходимо будет рассчитывать шанс выпадения предмета (current_chance) каждый раз при каждой попытке выдачи:

current_chance = (max — goods) / (length — tries)

Здесь max и length — константы, задаваемые тобой, наш друг гейм-дизайнер, и равные, соответственно, желаемому количеству получаемых игроком предметов (max) из желаемого количества попыток (length). Например, «max = 10 предметов из length = 100 попыток» (что будет эквивалентно 10% шансу выпадения по схеме, реализованной твоим неискушённым программистом). Две другие переменные (goods и tries) принимают значения, равные количеству уже выпавших на данный момент предметов (goods) из количества уже совершённых на данный момент попыток (tries). Как только tries становится равным length, всё начинается заново, и так по кругу.

Несложно подсчитать (если тебе сложно, смотри в таблице ниже), что в таком варианте реализации шанс успешной попытки растёт при каждой неудачной, пока не достигнет единицы (или 100%; для самых редких неудачников), и возвращается к базовому, равному max/length, при каждой следующей удачной попытке. И в конечном итоге, настроенная таким образом выдача будет гарантировать получение игроком 10 предметов из 100 попыток (не больше и не меньше).

Всё стало на свои места, и ожидания игроков совпали с реальностью, отлично. Но этого должно быть мало для настоящего пытливого гейм-дизайнерского ума! Поэтому мы зададим тебе дополнительный вопрос (со звездочкой) — а сможем ли мы проконтролировать выдачу 10 предметов из 100 попыток таким образом, чтобы игрок, например, чаще получал предметы на начальных попытках (и радовался, как ему благоволит «рандом») и реже на конечных (и не портил тебе расчеты экономики)? Нет-нет, не отвечай, это же обучающая статья, так что на все поставленные вопросы мы отвечаем сами. Ответ здесь простой — конечно же, сможем. Достаточно ввести в формулу магический коэффициент k следующим образом:

current_chance = ((max — goods) / ($length — $tries))*(k^(max — goods))

В итоге при k = 1 ничего в выдаче не изменится (и она будет равнораспределённой), при k > 1 игрок будет чаще получать предметы на начальных попытках, а при 0 < k < 1 — на конечных. Обманываем ли мы игрока? Конечно, обманываем. Становится ли ему от этого лучше? Конечно, становится. Получается ситуация, выигрышная для обеих сторон (побольше бы таких, вот тебе последняя на сегодня прописная истина).

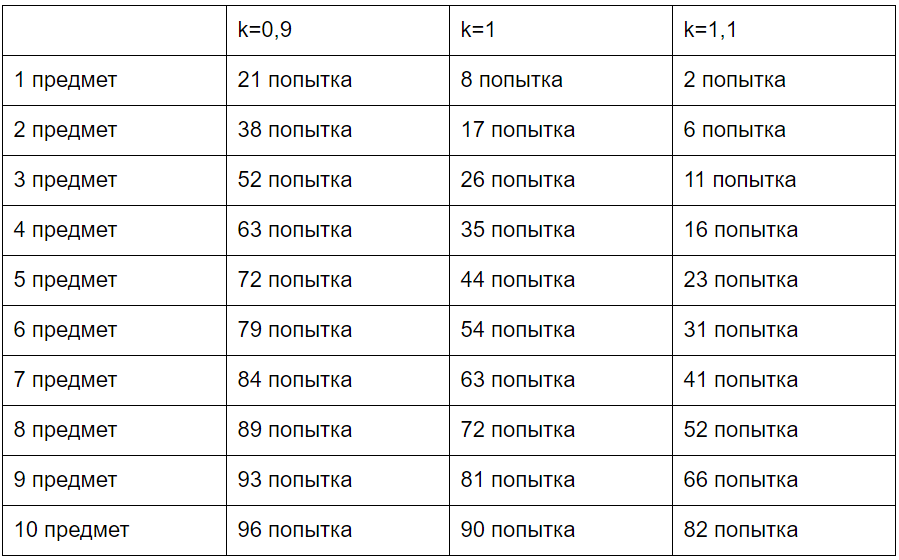
Ну а теперь танцы примеры. Ниже ты найдёшь таблицу, в которой для выпадения 10 предметов из 100 попыток и трёх разных значений коэффициента k посчитано, на какой попытке выпадет каждый предмет.

Надеемся, что ты не нарративщик и с этой таблицей все стало ещё понятнее, пока!