Игровой баланс #7

Последнее: тервер, обучение, заключение

Теория вероятностей

Самое частое применение тервера в геймдизайне: пугать молодых.

Поспешу успокоить: реально она почти не используется.

Возьмем известную задачу (иногда спрашивают на собеседованиях): из сундука с вероятностью 10% выпадает меч, какая вероятность получить меч, открыв 10 сундуков?

Правильный ответ: точно меньше 100%.
Для такого ответа достаточно головы на плечах — тервер не нужен.
Имея голову — все знания можно будет подтянуть под конкретную задачу.

Если все-таки вынуждают посчитать точную вероятность, отвечайте, что вы Байеса на Пуассоне вертели, вставайте и уходите.

В чем же тут подвох?

В том, что, делая баланс, вы моделируете усреднённое поведение игрока, а «шанс вытащить меч» — это чей-то конкретный сценарий. Скорее всего, этот шанс нам просто никогда не понадобится.
Вместо этого нам полезно знать «сколько мечей в среднем игрок вытащит из 100 сундуков».
А для этого тервер не нужен, сами понимаете.

Даже в случаях, когда точно нужна вероятность — вас может выручить простейший метод Монте-Карло, описанный Ником в новой статье.

Чисто для вашего успокоения приведу ответ про сундуки.
Это задача на вероятность хотя бы одного успеха среди N попыток.
Вычисляется так:
Шанс = 1 — ( 1 — Шанс 1 попытки) * <…> * ( 1 — шанс N-ой попытки)

В нашем случае шанс у всех попыток одинаковый, нам проще:
Шанс получить меч = 1 — ( 1–0.1)^10 = 1–0.9¹⁰ = 1–0.35 = 0.65, т.е. 65%

И небольшой совет

Есть несколько формул вероятности, которые применяются в разных ситуациях — в зависимости от числа попыток, постоянства шансов и так далее.
Учить формулы сами по себе — бессмысленно. Сначала нужно понять, какие они бывают и для каких ситуаций годятся. И разобраться в ситуации, ради которой нам понадобилось считать вероятность.

Очень может быть, что, хорошо подумав, вы и вовсе обойдетесь без тервера.

Кому не терпится разобраться глубже, рекомендую список типовых задач с решениями.
По ссылке будут примеры с разъяснениями, какая именно формула подходит и почему.
Про сами формулы можно почитать на Википедии.

Кривая обучения

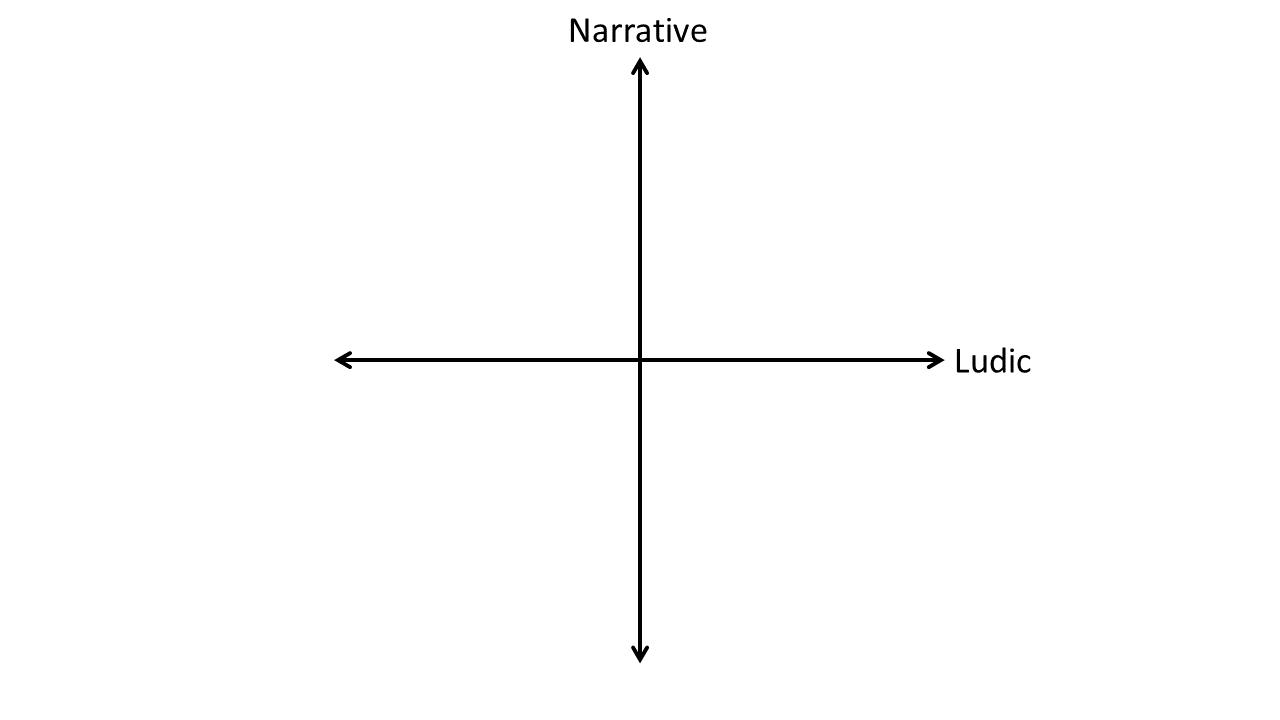
Кривая обучения (learning curve) — это график знакомства с новыми правилами, механиками, контентом.

Выглядит примерно так:

И не путайте с кривой сложности, про которую писал Ник.

У кривой обучения есть две задачи:

• Убедить нас, что на игрока не сваливалось слишком много нового, что заставит его напрягаться
• И наоборот: что в игре не будет длинных этапов, где нет ничего нового, а игрок может заскучать.

Если ваш контент распределён заведомо равномерно (например, все режимы открыты сразу, а новые шмотки появляются ровно каждый 5ый уровень) — в кривой обучения особого смысла нет.

В ином случае она может помочь и указать на проблемные этапы.

Делается так: берёте список уровней и для каждого уровня считаете, сколько контента (шмотки / карты / абилки ) на нём открывается.
А потом вручную вписываете «сложность освоения» новых механик (режимов, активностей, глобальных целей), которые появляются по мере игры. И строите график.
Пример:

Заключение

Итак, вы дочитали (или, вероятнее, прокрутили) до конца цикла про игровой баланс для начинающих геймдизов.

У меня стояла цель написать такой текст, который можно вручить любому тестеру, сценаристу или художнику одновременно с задачей «посчитай баланс моей игры».
И он посчитает, даже впервые в жизни открыв Excel.
Может быть, даже посчитает правильно.

Я старался избегать лишней обстоятельности и академичности, но при этом хотел упомянуть всё важное.
Важного оказалось больше, чем я думал.

Если вы знаете, как сделать этот текст лучше — что вырезать или чем дополнить и, что особенно важно, что было непонятно, что плохо описано или недостаточно раскрыто — пишите комментарии.

Содержание цикла про баланс:
— Введение и подготовка к работе
— Начало работы: константы и прогрессии
— Боевой баланс или расчет эффективности
— Матмодели и простая экономика
— Комплексная экономика: поведение и цикл
— Монетизация и экономика
— Дополнительно: тервер, кривая обучения, заключение